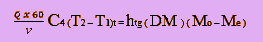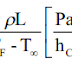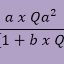LAMA PEMBEKUAN

Dalam mendisain sebuah proses pembekuan, penentuan waktu pembekuan merupakan hal yang sangat penting. Waktu pembekuan merupakan faktor kritis dalam pemilihan sistem pembekuan untuk mencapai kualitas pembekuan yang optimal.

1. Metode Plank

Persamaan Plank untuk menduga waktu pembekuan ditemukan oleh Plank (1913). Persamaan ini menggambarkan periode perubahan fase pada proses pembekuan untuk air.

dengan t_F adalah waktu pembekuan ; ρ adalah densitas produk beku ; L adalah panas laten pembekuan; T_F adalah suhu pembekuan ; T ͚ adalah suhu media pembeku; h_c adalah koefisien transfer panas konveksi; k adalah konduktivitas thermal produk ; a adalah ketebalan atau diameter produk ; P dan R adalah konstanta pengaruh bentuk bahan.

Jika produk tidak berbentuk lempeng, silinder, atau bola, Gambar 6.9 digunakan untuk menentukan konstanta. Koefisien β₁ adalah rasio panjang dan ketebalan produk. Koefisien β₂ adalah rasio lebar dan ketebalan produk.

Persamaan Planck (persamaan 8), tidak memperhitungkan waktu yang dibutuhkan untuk menghilangkan panas sensibel dari bagian produk yang tidak membeku pada saat di atas suhu awal pembekuan dan juga tidak memperhitungkan waktu yang dibutuhkan untuk menghilangkan panas sensible produk beku.

Persamaan Planck dimodifikasi :

Pengaruh dari panas sensibel di atas titik beku diakomodasi dengan bilangan

Planck :

Nilai konstanta P dan R ditentukan menggunakan grafik hubungan bilangan Planck dengan bilangan Stefan (Gambar 6.10 dan Gambar 6.11).

Bentuk dari produk ditetapkan menggunakan equivalent heat-transfer dimension (EHTD) :

Nilai W1 dan W2 ditetapkan dari Gambar 6.12 dengan menggunakan bilangan Biot dan faktor bentuk (β).

Nilai W1ditetapkan dengan menggunakan :

dengan d₁ adalah lebar produk dan d_c adalah ½ ketebalan produk.

Nilai W₂ ditetapkan dengan menggunakan :

dengan d₂ adalah panjang produk dan d_c adalah ½ ketebalan produk.

  2. Metode Pham

Pham (1986) memperkenalkan perbaikan persamaan Planck untuk memprediksi waktu pembekuan. Metode yang dikembangkan dapat digunkan untuk bahan yang bentuk tidak beraturan dengan pendekatan elipsoidal. Keunggulan dari metode ini adalah mudah digunakan dengan tingkat keakuratan yang dapat dipercaya. metode ini menggunakan asumsi sebagai berikut:

1.     Kondisi lingkungan adalah konstan

2.     Suhu awal , ti, konstan

3.     Nilai suhu akhir, tc, tetap

4.     Konveksi pada permukaan bahan mengukuti hukum newton tentang pendinginan.

dengan Ef adalah faktor bentuk : 1 untuk infinite slab ; 2 untuk infinite cylinder ; dan 3 untuk bola.

dengan : ρcu adalah densitas produk sebelum membeku ; Cpu adalah panas spesifik produk sebelum membeku; Ti adalah suhu awal produk ; Tfm adalah “mean freezing temperature” ; Tc adalah suhu akhir pada pusat produk ; T ͚ adalah suhu media pembeku ; ρF adalah densitas produk saat membeku ; dan CpF adalah panas spesifik produk saat beku.

Jika bentuk geometri produk bukan infinite slab, infinite cylinder, atau bola, maka digunakan β₁ dan β₂ (yang cara memperolehnya sama dengan pada metode Planck) :

dengan G1; G2; dan G3 diperoleh dari tabel :

SIFAT FISIK PRODUK BEKU

SIFAT-SIFAT FISIK PRODUK BEKU

1.     Densitas Produk

Pengaruh pembekuan terhadap densitas produk relatif kecil tetapi perubahan yang sangat signifikan terjadi hanya pada saat dibawah suhu pembekuan. Perubahan tersebut dapat diprediksi dengan persamaan yang dikemukakan Heldman (2001) :

dengan msi adalah berat masing-masing komponen bahan dan ρ_Si adalah berat jenis masing-masing komponen bahan.

2. Panas Spesifik Produk Beku

    Panas spesifik produk pangan beku dapat diprediksi menggunakan persamaan :

Persamaan (4) digunakan untuk memprediksi panas spesifik solid dari produk dengan mengabaikan fraksi air dari produk tersebut.    

3.     Konduktivitas Thermal Produk Beku

     Model persamaan untuk sistem dispersi dua komponen homogen :

dengan kL adalah konduktivitas thermal fase cair dan M_V² adalah fraksi volume fase diskontinyu pada produk (solid). Persamaan (5) digunakan jika konduktivitas thermal fase kontinyu (air) lebih besar dari konduktivitas thermal padatan (solid) produk.

     Jika konduktivitas thermal fase kontinyu dan diskontinyu pada produk sama, maka persamaannya :   

     dengan

  Persamaan (5) digunakan untuk memprediksi konduktivitas thermal produk pangan yang memiliki konduktivitas thermal air pada produk lebih besar dari konduktivitas thermal solid produk tersebut.

    

    Untuk produk dengan kadar air rendah, maka air bukan lagi fase kontinyu. Untuk produk dengan kadar air rendah, persamaan (6) dan (7) adalah model yang tepat untuk memprediksi konduktivitas thermal.

4. Entalpi Produk

   Pada proses pembekuan terjadi penurunan suhu bahan sampai ke titik yang diinginkan, sehingga akan terjadi penubahan nilai enthalpinya. Perubahan nilai enthalpi total atau nilai panas dibutuhkan untuk menurunkan suhu bahan dari titik di atas titik bekunya sampai suhu penyimpanan yang diinginkan.

    

PENENTUAN TITIK BEKU DAN FRAKSI TIDAK BEKU

Termodinamika dapat digunakan untuk menggambarkan perubahan fisik dalam air dalam suatu produk makanan selama proses pembekuan.

 PENURUNAN TITIK BEKU

Hubungan antara komposisi produk dan suhu telah diinterpretasikan oleh Heldman (1974) dan Schwartzberg (1976) dalam persamaan sebagai berikut:

dengan (X_A) adalah fraksi mol air dalam produk, (T_A) adalah suhu kesetimbangan pembekuan, (λ) adalah panas laten molar peleburan, dan (R_g) adalah tetapan gas.

     Fraksi mol air dalam produk dapat didefinisikan sebagai berikut:

dengan (m_A) adalah berat air dalam bahan; (M_A) adalah berat molekul air dalam bahan; (m_SI) adalah berat komponen produk; dan (M_SI) adalah berat molekul komponen produk.

Contoh Soal :

Komposisi orange juice adalah air 88,3 %; protein 0,7 %; karbohidrat 10,4 %; lemak 0,2 %; dan abu 0,4 %. Panas laten pelelehan es adalah 333,5 J/g dan konstanta gas universal 8,3144 J/mol K. Estimasikan penurunan suhu pembekuan kesetimbangan dari produk tersebut !

Jawab :

1. Komposisi dan berat molekul komponen produk (USDA, 2004) :

2. Dengan menggunakan persamaan (2), maka didapatkan :

3. Dengan persamaan (1), maka didapatkan :

FRAKSI AIR TIDAK BEKU

Salah satu karakteristik unik dari pembekuan makanan adalah hubungan antara fraksi air tidak membeku dan suhu. Hubungan tersebut merupakan dasar untuk merancang sistem pembekuan dan fasilitas penyimpanan beku pada produk pangan.

Fraksi air yang tidak membeku dalam produk pangan akan menurun secara bertahap karena suhu turun di bawah suhu pembekuan awal. Hubungan tersebut dapat dideskripsikan dengan persamaan (1) dan (2)

Contoh Soal :

Hitunglah persentase air yang tidak membeku pada strawberi beku pada suhu – 10 °C! Panas laten pelelehan es adalah 333,5 J/g dan konstanta gas universal 8,3144 J/mol K. Komposisi strawberi sebagai berikut :

Jawab :

Menggunakan persamaan (1) dengan T_A = - 10 °C atau 263 K

Menggunakan persamaan (2), maka diperoleh :

Fraksi massa air yang tidak membeku adalah 0,06642, sehingga persentase air yang tidak membeku :

PENGANTAR ANALISIS SISTEM PENGERINGAN ALAS TETAP

Pada bab-bab sebelumnya tentang prinsip psikometrik, kadar air kesetimbangan dan aliran udara telah dibahas. Bab ini berisi pengembangan prinsip-prinsip tersebut diatas menjadi analisis yang disederhanakan tentang pengeringan bijian dengan alas tetap. Analisis ini menggunakan persamaan kesimbangan panas sederhana yang memungkinkan perhitungan yang berhubung dengan waktu pengeringan, air yang dibuang dan sifat-sifat daerah pengeringan.

Proses Pengeringan

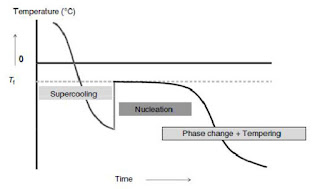
Gambar 7.1 adalah kurva dari proses pengeringan alas tetap. Udara pengering bergerak dari dasar ke alas-alas. Pertukaran kadar air dari biji ke udara terjadi pada kedalaman yang tetap atau pada daerah bijian. Pada awal proses pengeringan, daerah pengeringan terdapat pada dasar alas. Setelah pengeringan berlangsung terus, daerah ini bergerak keatas, dan bila daerah ini telah melampaui semua bijian, keseluruhan massa bijian dikeringkan dalam keseimbangan dengan udara pengering.

Bijian dibawah daerah pengeringan mencapai kondisi kesetimbangan dengan udara yang masuk dan memiliki kandungan air sebesar M_e. Bijian diatas daerah pengeringan belum mulai mengalami pengeringan dan tetap mempunyai kadar air sebesar M_o. Udara yang melewati bijian diatas daerah pengeringan dalam kesetimbangan dengan kadar air awal bijian. Saat melewati daerah pengeringan, udara membawa uap air secara evaporasi dan didinginkan dengan proses evaporasi dari T_a ke T_g.

   Terdapat 2 gradien yang melintasi daerah pengeringan:

1.                Gradien kadar air dari M_e ke M_o

2.                Gradien suhu dari T_e ke T_g.

Jika alas bijian adalah dangkal dan atau kecepatan udara adalah tinggi, daerah pengeringan biji berkembang meliputi seluruh alas, rata-rata kadar air akhir yang diinginkan bisa dicapai sebelum lapisan biji bawah mencapai kesetimbangan dengan udara pengering.

 

Kesetimbangan Panas Untuk Pengeringan

Bagian berikut ini membahas berbagai elemen dari persamaan (7.1)

 

            Pada persamaan (7.1) dianggap bahwa panas sensibel yang ditangkap oleh udara yang melewati biji sama dengan panas laten penguapan yang diperlukan untuk menguapkan air dari bijian. Persamaan ini tidak mempertimbangkan perubahan suhu bijian yang terjadi bila udara lebih panas atau lebih dingin dibandingkan bijian pada saat mulai operasi. Juga persamaan (7.1) tidak mempertimbangkan kondensasi yang mungkin terjadi pada lapisan atas bijian pada saat mulai operasi pengeringan, atau perubahan kondisi sekitar. 

PARAMETER PARAMETER PERSAMAAN KESETIMBANGAN PANAS (7.1) :

Laju Aliran Udara

Laju aliran udara (Q) melalui suatu sistem pengeringan bisa diperoleh dengan menggambar kurva sistem versus kursa kipas angin, seperti telah dijelaskan pada bab 6. Laju aliran udara ke sistem yang bekerja bisa juga diperoleh dengan pengukuran tekanan statis pada sistem dan menghitung aliran udara dari tekaan.

Suhu Udara Dan Volume Spesifik

Volume spesifik udara (v) dan penurunan suhu melalui massa bijian (Tn – Tg) diperoleh dari diagram psikrometrik. Sebelum nilai-nilai ini dapat ditentukan, dipilih kondisi udara sekitar daerah tersebut serta musim yang berlaku. Nilai yang ini mempunyai pengaruh penting pada perhitungan-perhitungan, terutama bila udara biasa digunakan untuk pengeringan.

Peta Suhu Bola Basah

Waite and Bern (1987) dan Schmidt and Waite (1962) menggambarkan peta-peta daerah di Amerika Serikat dan Kanda Selatan yang menunjukkan garis-garis dengan suhu sama untuk tiap bulan dalam satu tahun dari rata-rata suhu bola basah dan rata-rata penurunan suhu bola basah beserta simpangan bakunya.

Suhu Udara Plenum dan Volume Spesifik

          Kondisi udara pada plenum yang merupakan masukan (input) pada persamaan (7.1) tergantung pada apakah udara telah mengalami pemanasan. Selama pengeringan udara alami, udara tidak dipanaskan dan kondisi plenum dan sekitarnya dianggap sama.

Kondisi Udara Luar

          Pada bab 4, data kadar air kesetimbangan ditunjukkan sebagai garis-garis dengan suhu yang sama pada gambar kadar air versus kelembaban relatif. Pada analisis pada bab ini, penting sekali untuk menggabungkan data pada diagram psikrometrik sebagai kurva kelembaban kesetimbangan kadar sama.

Panas Penguapan

Panas yang diperlukan untuk menguapkan satu pound air dari bijian adalah merupakan fungsi kadar air bijian dan suhu dimana terjadi penguapan. Melintasi daerah pengeringan, penguapan terjadi pada suhu dan kadar air biji yang berubah terus menerus. Oleh sebab itu nilai panas penguapan juga berubah terus. Panas penguapan  tertinggi terjadi pada bagian bawah dari daerah pengeringan dimana kadar air bijian adalah paling rendah dan  panas penguapan paling rendah terjadi pada bagian atas dari daerah pengeringan dimana kadar air bijian adalah tertinggi.

Bahan Kering

Pada persamaan (7.1), DM adalah jumlah bahan kering didalam wadah. Jika kehilangan bahan kering karena diabaikan, kandungan bahan kering akan sama pada awal dan akhir proses pengeringan. Oleh sebab itu, penting sekali jumlah bahan kering awal pada proses pengeringan dapat dihitung.

Kadar Air Bijian

Pernyataan kadar air M_e dan M_o (berbasis kering, desintal) menyatakan kadar air pada awal pengeringan dan kadar air saat bijian mencapai kesetimbangan dengan kondisi udara pada plenum (M_e). Bila pengeringan dilaksanakan pada alas yang dalam (beberapa kali dari kedalaman daerah pengeringan), daerah pengeringan berada di atau dekat bagian atas massa bijian pada akhir operasi dan keseluruhan massa bijian mempunyai kadar air.

Penggunaan Persamaan (7.1)

Contoh 7.2 :

            Wadah berdiameter 27 ft diisi sedalam 8ft dengan jagung pipil dengan kadar air 12.5% basis basah. Wadah ini terletak di Ames, lowa. Tekanan statis diukur pada kedalaman ft dari permukaan bijian dan tercatat 0.31 inchi air. Hitung waktu pengeringan jika digunakan udara tidak dipanaskan pada bulan september.

Penyelesaian 7.2 :

Aliran udara adalah ΔP = 0.93 inchi air/ 3 ft = 0.31 inchi air/ft

Dari kesamaan (6.2). aliran udara adalah 28.5 cgm/ft2

Total cfm        = 28.5 cfm/ft2 x luas lantai (ft2)

= 28.5 x 573 = 16330 cfm

Kondisi udara sekeliling yang dibaca dari peta schmidt and waite (gambar c-2) adalah : Tab = 57.2ͦ F dan penurunan suhu bola basah = 63.5ͦ F.C = 0.24 Btu/lbͦ F dan hfg = 1.200 Btu/lb. Kondisi udara pada plenum dari diagram psikrometrik.

            Ta = 63.5ͦ F, φa = 67%, v= 13.60 ft3/lb

Analisis Sistem Pengeringan Alas Dalam

Kurva pada gambar 7.4 diciptakan Hukill (1947, 1954). Kurva ini dinamakan kurva pengeringan “total” dan dapat digunakan untuk kadar air pada seberang kedalaman bijian pada sistem pengeringan dengan dalam pada setiap saat setelah pengeringan dimulai.

Perbandingan Kadar Air

          Pernyataan matematik untuk kura pada gambar 7.4 dinyatakan dengan persamaan (7.2)  

Dimana : MR = (M-Me) / (M_o-M_e)

Faktor Kedalaman

            Salah satu faktor kedalaman berisi jumlah bahan kering yang dapat dihitung dengan kesetimbangan panas yang mirip dengan persamaan (7.1). Dalam hal ini, t dibuat sama dengan t2 dan DM’ dihitung:

Satuan Waktu 

 

Daerah Pengeringan

            Kurva pada gambar 7.4 menduga pendekatan terhadap M_o dan M_e sebagai suaru “asimtot”. Dari kurva ini akan sulit untuk menyatakan kapan kadar air bijian mulai jatub dibawah M_o atau kapan M_e. Untuk menghilangkan keraguan, kita anggap daerah pengeringan berisi 13 faktor kedalaman.

 

Pengaruh T1/2

 

Sumber :  Brooker, D. B dan Bakker, F.W. 1974. Pengeringan Dan Penyimpanan Biji-Bijian Dan Biji Minyak Nabati, Terjemahan Rahmad Hari Purnomo tahun 1997. Indralaya : Fakultas Pertanian, Universitas Sriwijaya